Animate intermediate results of your algorithm

Posted on Tue 19 February 2019 in machine learning • 5 min read

This post is part 6 of the "clustering" series:

The R package gganimate enables to animate plots. It is particularly interesting to visualize the intermediate results of an algorithm, to see how it converges towards the final results. The following illustrates this with K-means clustering.

The outline of this post is as follows: We will first generate some artificial data to work with. This allows to visualize the behavior of the algorithm. The k-means criterion and an algorithm to optimize it is then presented and implemented in R in order to store the intermediate results in a dataframe. Last, the content of the dataframe is ploted dynamically with gganimate.

Generate some data

To see how the algorithm behaves, we first need some data. Let's generate an artificial dataset:

library(mvtnorm)
library(dplyr)

generateGaussianData <- function(n, center, sigma, label) {
  data = rmvnorm(n, mean = center, sigma = sigma)
  data = data.frame(data)
  names(data) = c("x", "y")
  data = data %>% mutate(class=factor(label))
  data
}

dataset <- {
  # cluster 1
  n = 50
  center = c(5, 5)
  sigma = matrix(c(1, 0, 0, 1), nrow = 2)
  data1 = generateGaussianData(n, center, sigma, 1)

  # cluster 2
  n = 50
  center = c(1, 1)
  sigma = matrix(c(1, 0, 0, 1), nrow = 2)
  data2 = generateGaussianData(n, center, sigma, 2)

  # all data
  data = bind_rows(data1, data2)
  data$class = as.factor(data$class)
  data
}

We generated a mixture of two Gaussians. There is nothing very special about it, except it is in two dimensions to make it easy to plot it, without the need of a dimensionality reduction method.

Let's now move on to our algorithm.

K-means

Here, I choose to use k-means since it is widely used for clustering, and moreover, results in a simple implementation.

For a given number of clusters K, and a set of N vectors \(x_i , i \in [1, N]\), K-means aims to minimize the following criterion:

\begin{equation*} W(z, \mu) = \sum_{k=1}^{K} \sum_{i=1}^{N} z_{ik} ||x_i - \mu_k||^2 \end{equation*}

with:

\(z_{ik} \in {0, 1}\) indicates if the vector \(x_i\) belongs to the cluster \(k\);
\(\mu_k \in \mathbb{R}^p\), the center of the cluster \(k\).

Llyod and Forgy algorithms

Several algorithms optimize the k-means criterion. For instance, the R function kmeans() provides four algorithms:

kmeans(x, centers, iter.max = 10, nstart = 1,
       algorithm = c("Hartigan-Wong", "Lloyd", "Forgy",
                     "MacQueen"), trace=FALSE)

In fact, Forgy and Lloyd algorithms are implemented the same way. We can see this in the source code of kmeans():

edit(kmeans)

It opens the source code in your favorite text editor. At lines 56 and 57, "Forgy" and "Lloyd" are assigned to the same number (2L) and are thus mapped to the same implementation:

nmeth <- switch(match.arg(algorithm), `Hartigan-Wong` = 1L,
    Lloyd = 2L, Forgy = 2L, MacQueen = 3L)

In the following, we will implement this algorithm. After the initilization, it iterates over two steps until convergence:

an assignment step which assigns the points to the clusters;
an update step which updates the centroids of the clusters.

Initialization

The initialization consists in selecting \(K\) points at random and consider them as the centroids of the clusters:

dataset = dataset %>% mutate(sample = row_number())
centroids = dataset %>% sample_n(2) %>% mutate(cluster = row_number()) %>% select(x, y, cluster)

Assignment step

The assignment step of k-means is equivalent to the E and C step of the CEM algorithm in the Gaussian mixture model. It assigns the points to the clusters according to the distances between the points and the centroids. Let's write \(z_k\) the set of points in the cluster \(k\):

\begin{equation*} z_k = \left\{ i; z_{ik} = 1 \right\} \end{equation*}

We estimate \(z_k\) by:

\begin{equation*} \hat{z}_k = \{ i; ||x_i - \mu_k||^2 \leq ||x_i - \mu_{k'}||^2; k' \neq k \} \end{equation*}

A point \(x_i\) is set to be in the cluster \(k\) if the closest centroid (using the euclidean distance) is the centroid \(\mu_k\) of the cluster \(k\). This is done by the following R code:

assignmentStep = function(samplesDf, centroids) {
  d = samplesDf %>% select(x, y, sample)
  repCentroids = bind_rows(replicate(nrow(d), centroids, simplify = FALSE)) %>%
    transmute(xCentroid = x, yCentroid = y, cluster)
  d %>% slice(rep(1:n(), each=2)) %>%
    bind_cols(repCentroids) %>%
    mutate(s = (x-xCentroid)^2 + (y-yCentroid)^2) %>%
    group_by(sample) %>%
    top_n(1, -s) %>%
    select(cluster, x, y)
}

Update step

In the update step, the centroid of a cluster is computed by taking the mean of the points in the cluster, as defined in the previous step. It corresponds to the M step of the Gaussian mixture model and it is done in R with:

updateStep = function(samplesDf) {
  samplesDf %>% group_by(cluster) %>%
    summarise(x = mean(x), y = mean(y))
}

Iterations

Let's put together the steps defined above in a loop to complete the algorithm. We define a maximum number of iterations maxIter and iterate over the two steps until either convergence or maxIter is reached. It converges if the centroids are the same in two consecutive iterations:

maxIter = 10
d = data.frame(sample=c(), cluster=c(), x=c(), y=c(), step=c())
dCentroids = data.frame(cluster=c(), x=c(), y=c(), step=c())
for (i in 1:maxIter) {
  df = assignmentStep(dataset, centroids)
  updatedCentroids = updateStep(df)
  if (all(updatedCentroids == centroids )) {
    break
  }
  centroids = updatedCentroids
  d = bind_rows(d, df %>% mutate(step=i))
  dCentroids = bind_rows(dCentroids, centroids %>% mutate(step=i))
}

The above R code constructs two dataframes d and dCentroids which contain respectively the assignations of the points and the centroids. The column step indicates the iteration number and will be used to animate the plot.

Plot

We are now ready to plot the data. For this, ggplot2 is used with some code specific to gganimate:

library(ggplot2)
library(gganimate)

a <- ggplot(d, aes(x = x, y = y, color=factor(cluster), shape=factor(cluster))) +
  labs(color="Cluster", shape="Cluster", title="Step: {frame} / {nframes}") +
  geom_point() +
  geom_point(data=dCentroids, shape=10, size=5) +
  transition_manual(step)
animate(a, fps=10)
anim_save("steps.gif")

The function transition_manual of gganimate allows to animate the plot by filtering the dataframe at each step given the value of the column passed as parameter (here step). The variables frame and nframes are provided by gganimate and are used in the title. They give the number of the current frame and the total number of frames respectively.

The animate function takes the argument fps which stands for "frames per second". This call takes some time to process since it generates the animation. The animation is then stored in "steps.gif":

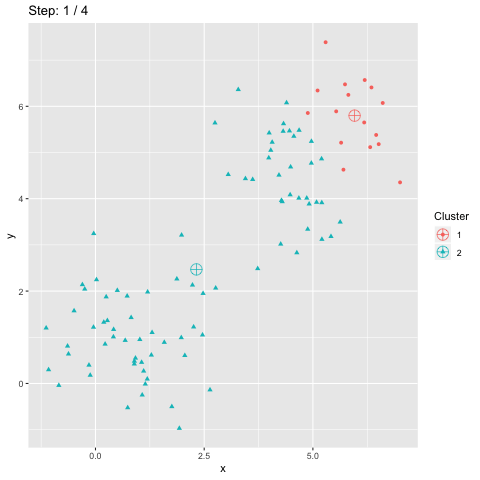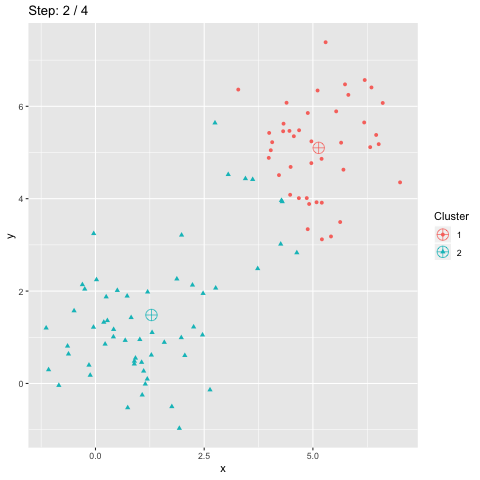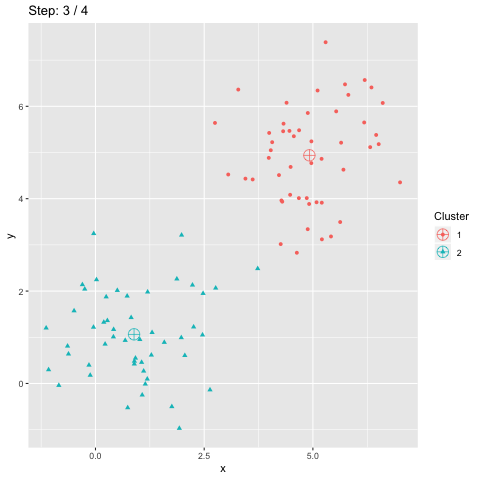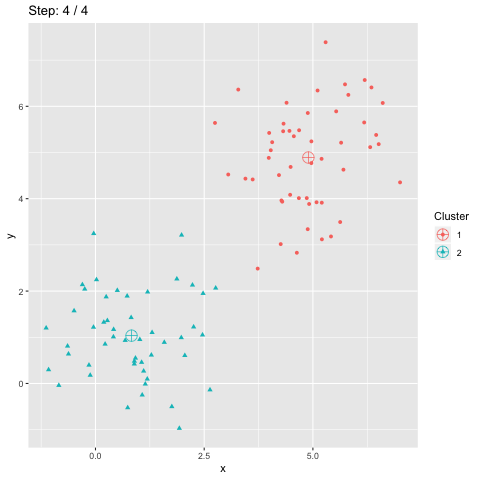
To sum up

This post gives an example of how to use gganimate to plot the intermediate results of an algorithm. To do this, one have to:

import gganimate;
create a dataframe with an additional column which stores the iteration number;
create a standard ggplot2 object;
use the transition_manual function to specify the column used for the transition between the frames (the iteration number);
generate the animation with animate;
save the animation with anim_save.

We also covered the Lloyd and Forgy algorithms to optimize the k-means criterion.

Looking at the implementation of R functions is sometimes helpfull. For instance we looked at the implementation of k-means to see that two algorithms proposed as arguments are in fact the same.

Previous Post Next Post